Kerucut adalah salah satu bangun ruang yang mempunyai sisi lengkung. Dalam pelajaran matematika, penting bagi siswa memahami rumus luas permukaan kerucut dan cara mengaplikasikannya dalam contoh soal.
Di kehidupan sehari-hari begitu banyak benda berbentuk kerucut. Sebut saja kap lampu, caping (sejenis topi dari anyaman bambu) dan cetakan tumpeng. Sebagai informasi kerucut adalah bangun ruang yang amat istimewa karena memiliki bentuk alas lingkaran dengan sebuah titik puncak.
Ciri Bangun Ruang Kerucut
Melansir modul Matematika terbitan Kemendikbud oleh Dwi Ari Noerharijanti, S.T., dkk, terdapat ciri-ciri bangun ruang kerucut yaitu sebagai berikut:
- Tersusun oleh 2 buah sisi, yaitu lingkaran dan sebuah sisi lengkung.
- Sisi yang berbentuk lingkaran merupakan alas kerucut.
- Sisi yang berbentuk bidang lengkung membentuk selimut kerucut.
- Bidang lengkung pada kerucut merupakan juring lingkaran (sektor).
- Kerucut mempunyai 1 rusuk dan satu titik puncak.
Apabila sebuah kerucut dibuka dan dibedah, maka akan membentuk jaring-jaring kerucut yang terdiri dari selimut kerucut (sisi lengkung) dan tutup kerucut. Jarak titik puncak ke atas disebut tinggi kerucut.
Artikel terkait: Mengenal Rumus Luas Belah Ketupat, Sifat-sifat, Unsur, dan Contoh Soalnya
Menghitung Rumus Luas Permukaan Kerucut
Mengingat alas bangun kerucut adalah lingkaran dan memiliki kemiripan dengan tabung maka selimutnya bersisi tegak.
Untuk itu, dengan mensubstansi luas lingkaran S = πr² dan keliling lingkaran 2πr. Sehingga luas permukaan kerucut dapat dicari dengan cara: luas alas + luas selimut
L = (π x r²) + (π x r x s )
L = Luas permukaan kerucut
π = phi, bisa bernilai 22/7 atau 3,14
r = jari-jari alas lingkaran
s = garis pelukis
t = tinggi kerucut
Contoh Soal Luas Permukaan Kerucut
Dengan mengetahui rumus, saatnya memahami menghitung kerucut dalam bentuk soal. Berikut contoh soalnya.
1. Diketahui kerucut mempunyai alas dengan jari jari lingkaran 5 cm, garis pelukis (s) = 13 cm dan tinggi 12 cm. Hitunglah luas permukaan dari kerucut tersebut!
L = (π x r²) + (π x r x s )
= (3,14 x 52) + (3,14 x 5 x 13)
= 78,5 + 204,1
= 282,6 cm²
Jadi, rumus luas permukaan kerucut tersebut adalah 282,6 cm².
2. Cetakan nasi tumpeng berbentuk kerucut memiliki diameter 16 cm, dengan jari jari r= 8 cm dan tinggi t=15 cm. Panjang garis pelukisnya adalah…
L = πr (r+s) → rumus luas permukaan tabung
= π(8) (8+17) → substansi nilai r dan t
= 200 cm²
Jadi, luas permukaan dari cetakan nasi tumpeng yang berbentuk kerucut adalah 200 cm².
Artikel terkait: Mengenal Rumus Keliling Persegi dan Aplikasinya dalam Bentuk Soal
3. Jari-jari alas sebuah kerucut adalah 6 cm. Jika tinggi kerucut adalah 8 cm, hitung luas selimut kerucut dan luas permukaan kerucut.
Diketahui: r = 6 cm; t = 8 cm; π = 3,14
Pertama, cari panjang garis pelukis kerucut sebagai berikut s= √r2 + t2 = √62 + 82 = √100 = 10.
Maka, luas selimut kerucut = πrs = 3,14 × 6 × 10 = 188,4.
Luas selimut kerucut adalah 188,4 cm2.
Luas permukaan kerucut = luas selimut + luas alas = 188,4 + (πr2)
Luas permukaan kerucut = 188,4 + (3,14 × 6 × 6) = 301,44 cm2.
4. Diketahui jari-jari alas sebuah kerucut adalah 3,5 cm dan tingginya 12 cm. Berapakan luas sisi kerucut tersebut?
Pembahasan: Diketahui r =3,5 cm; t = 12 cm, π = 22/7
Pertama, cari nilai s menggunakan rumus garis pelukis. s2 = r2 + t2 s2 = 3,52 + 122 s2 = 156,25 s = 12,5 cm
Maka luas sisi kerucut = πr (s+r) = 22/7 × 3,5 (12,5 +3,5) = 176 cm2
Dengan demikian, luas sisi kerucut tersebut adalah 176 cm3.
5. Diameter sebuah kerucut adalah 10 cm dan tingginya 12 cm, tentukanlah panjang apotema (s), luas selimut kerucut, luas permukaan:
Diketahui:
d = 10 maka r = 5 cm, t = 12 cm
Ditanya:
a. Panjang garis pelukis (s)
b. Luas selimut kerucut
c. Luas permukaan kerucut
Penyelesaian:
a. Panjang garis pelukis (s)
s2 = t2 + r2
= 122 + 52
= 144 + 25 = 169
s = 13
Jadi, panjang garis pelukis kerucut tersebut adalah 13 cm.
b. Luas selimut kerucut = πrs
Ls = 3,14 x 5 x 13
Baca juga: Daftar Kumpulan Rumus Fisika yang Sering Digunakan di Ujian [TERLENGKAP]
= 204,1
Jadi, luas selimut kerucut tersebut adalah 204,1 cm2.
c. Luas permukaan kerucut = πr (s + r)
L = 3,14 x 5 x (13 + 5)
L = 282,6
Jadi, luas permukaan kerucut tersebut adalah 282,6 cm2
6. Hitunglah jari-jari kerucut yang mempunyai tinggi 20 cm dan luas permukaan 2640 cm²…
Diketahui:
t = 20 cm
L = 2640 cm²
Ditanya:
Jari-jari kerucut (r)
Penyelesaian:
Untuk dapat membentuk faktor persamaan, dihitung terlebih dahulu panjang garis pelukis (s),
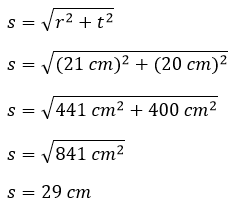
Kemudian substitusi nilai s = 29 ke persamaan berikut,
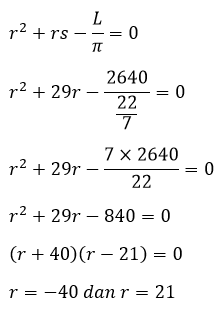
Dari hasil faktor persamaan dapat diuji
r = -40 cm tidak memenuhi syarat, karena hasil luas permukaan akan bernilai negatif atau tidak sama 2640 cm²
r = 21 cm memenuhi syarat, karena hasil hasil luas permukaan bernilai 2640 cm².
Jadi, jari-jari kerucut adalah 21 cm.
Demikian ulasan mengenai rumus luas permukaan kerucut, semoga dapat membantu si kecil mengerjakan PR di rumah dengan lancar!
***
Baca juga:
Rumus Luas Permukaan Kubus, Lengkap dengan Contoh Soal
Mengulik Rumus Volume Kubus Lengkap dengan Contoh Soalnya
Mengenal Hukum Archimedes Beserta Rumus dan Penerapannya di Kehidupan
Parenting bikin pusing? Yuk tanya langsung dan dapatkan jawabannya dari sesama Parents dan juga expert di app theAsianparent! Tersedia di iOS dan Android.
Kehamilan
Anak
Perkembangan Otak
Rangkaian Edukasi
TAPpedia
TAP Rekomendasi
Parenting
Kesehatan
Gaya Hidup
Nutrisi
Ayah manTAP!
Komunitas
VIP
Event
Hadiah
VIP Parents
